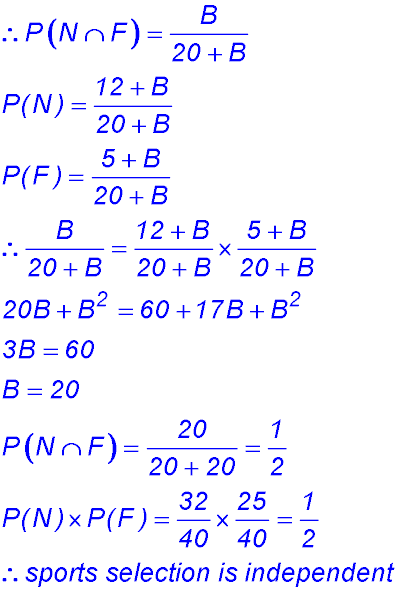1. The events:

(i) Throwing a 3 with a dice and selecting a King from a deck of cards. INDEPENDENT.
There is no relationship between them.

(ii) Catching a fish and wearing a lucky T-shirt.
INDEPENDENT.
There is no relationship between them.

(iii) Watching your favourite team win and sitting in a lucky seat.
INDEPENDENT.
There is no relationship between them.

(iv) Studying for a Maths test and obtaining a good result.
DEPENDENT.
More study of an enjoyable subject leads to greatly enhanced results (and increased happiness).

3.

• 10% of developing a headache and becoming dizzy;
• 25% of developing a headache only;
• 60% of becoming dizzy only.

If the two outcomes of headache (H) and dizziness (D) are independent, then P(H∩D) = P(H) P(D).

P(H∩D) = = 10%

P(H) = 25%

P(D) = 60%

P(H) × P(D) = 15% which is not 10% - so not independent.

P(A∩B) = P(A)P(B).

As P(A) = 2P(B) then P(A∩B) = 2[P(B)]².
So now we have to link the intersection and union terms:

P(A∪B) = 0.52 = P(A) + P(B) - P(A∩B).

∴ 0.52 = 3P(B) -  2[P(B)]².

2[P(B)]² - 3P(B) + 0.52 = 0

Using the quadratic formula to solve for P(B) gives:

P(B) = 1.3 (not possible) and P(B) = 0.2.

∴ P(A) = 0.4.

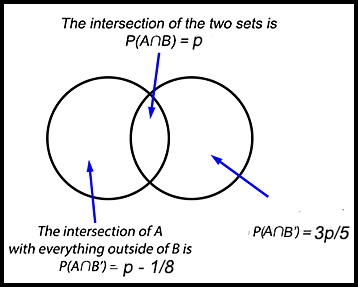
5. For events A and B, P(A∩B) = p, P(A'∩B) = p - 1/8
and P(A∩B') = 3p/5.

If A and B are independent, determine the value of p.

7. We know that for independence P(A∩ B) = P(A)×P(B).
But here we need to calculate the total number of girls to change the given frequencies into probabilities.

Well there are 12 + 5 + B + 3 = 20 + B girls. We can therefore divide the frequencies:

A local supermarket was reviewing its operations. It wanted to improve its customer relations and, as part of that review, decided to determine when customers were most likely to visit the store

• on weekdays or weekends; and
• whether the customers came in before 5 pm or after 5 p.m.

The researcher developed the following table:

Three percentages from the review are entered into the above table together with the total percentage or respondents.

(i) Complete the percentage entries in the table.

(ii) By converting the percentages to probabilities, evaluate the conclusion that time of shopping and day of the week are independent events.